Confusion and diffusion – Block Ciphers and Their Modes of Operation
14.2.2 Confusion and diffusion
What makes a good block cipher? Claude Shannon was perhaps the first to try and answer this question in a systematic way [162]. He defined two methods for frustrating a statistical analysis:
- Assuming that a meaningful plaintext must exhibit some statistical structure, he suggested that the cipher should dissipate this structure over the entire ciphertext. This principle is called diffusion. Generally, it can be achieved by permuting the symbols in the plaintext block.
- Simply permuting the symbols in a plaintext block will destroy local patterns, but the global plaintext statistics will remain unchanged (for example, permuting the pixels in an image does not change its histogram). In order to obscure the global plaintext statistics, the ciphertext should depend on the plaintext in a very complex way. This principle is called confusion. In practice, this principle is realized by a complex substitution of the plaintext symbols.
A good block cipher will contain both components. In order to not give any hints about the plaintext statistics, the substitution and permutation components need to look random, that is, as if having no structure, to the attacker. We will now look at this requirement in detail.
14.2.3 Pseudorandom functions
We start with pseudorandom functions that we briefly touched upon in Chapter 4, Encryption and Decryption. Roughly speaking, a pseudorandom function is a deterministic function that appears to be random to any polynomial-time adversary.
Conceptually, a pseudorandom function is a generalization of a pseudorandom generator [97] in that it involves random-looking functions instead of random-looking strings. Technically speaking, pseudorandomness is a property of a distribution of functions obtained using keyed functions. Recall that a keyed function is a two-argument function of the form:
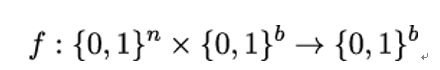
where the first input is the key k. Typically, the key k ∈{0,1}n is chosen and fixed to obtain a single-input function fk : {0,1}b →{0,1}b. Let fb denote the set of all functions having the same domain and range {0,1}b. A keyed function induces a distribution on functions in fb. The distribution is determined by choosing uniformly a key k ∈{0,1}n. This selects a specific function fk from fb.
The keyed function f is called pseudorandom if an efficient adversary cannot distinguish the function fk from a function f chosen uniformly at random from the set fb. In other words, no polynomial-time adversary should be able to tell whether it is interacting with fk or with f. The term interacting refers to the fact that the formal definition of a pseudorandom function (see, for instance, [97]) gives the adversary – oftentimes referred to as a probabilistic polynomial-time distinguisher in the cryptographic literature – access to an oracle that takes any input x and returns the function value for x. Because both functions fk and f are deterministic (they are only chosen randomly), the oracle returns the same result when it is presented with the same input x. However, if f is a pseudorandom function, no polynomial-time adversary can tell whether the oracle returns fk(x) or f(x).
Note that pseudorandomness is not a trivial property for a keyed function f because the set fb, the set of all functions having the same domain and range {0,1}b, has (2b)2b = 2b⋅2b functions (for each of the 2b inputs, there are 2b possible outputs).
On the other hand, because there are 2n keys, fk is chosen from a distribution of at most 2n distinct functions [97]. Yet, the behavior of fk and a randomly chosen function f ∈ fb must appear the same for any polynomial-time adversary.
From the theoretical perspective, cryptographers believe that block ciphers behave like pseudorandom functions. More precisely, they are assumed to behave like a specific type of pseudorandom functions, namely, pseudorandom permutations.
