Key scheduling – Block Ciphers and Their Modes of Operation
14.3.3 Key scheduling
As a round key is added to the 128-bit plaintext block before the first encryption round and at the end of each encryption round, the AES key k needs to be expanded into r + 1 different round keys ki, where each round key has 128 bits and r ∈{10,12,14}.
Suppose k has 128 bits. In this case, we are going to do 10 rounds, so we need 11 round keys of 128 bits each. We start by separating k into four 32-bit words W0,W1,W2,W3. Then the key is expanded by generating more words Wi for 4 ≤ i ≤ 43 by the following algorithm:
- If i ≥ 4 is not a multiple of four, then
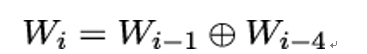
- If i ≥ 4 is a multiple of four, then Wi−1 is first transformed by shifting its four bytes (a,b,c,d) cyclically to the left by one place to get (b,c,d,a). Then SubBytes is applied on each of the bytes and a constant round word cℓ is added. The round word is an element of (𝔽2[X]∕M)4, that is, it consists of four bytes, where each byte is an element of 𝔽2[X]∕M, the same finite field as where the elements of the state matrix live. For 128-bit key length, the cℓ are defined by
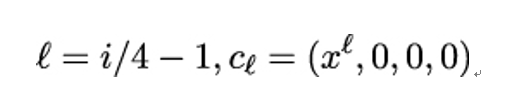
In case you don’t want to go through the algebra for yourself, here is a table with the cℓ written in hexadecimal form:
| ℓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| cℓ | 01 | 02 | 04 | 08 | 10 | 20 | 40 | 80 | 1B | 36 |
Table 14.1: Hexadecimal round constants in an AES key schedule
Thus, if Wi−1 = (a,b,c,d), we get
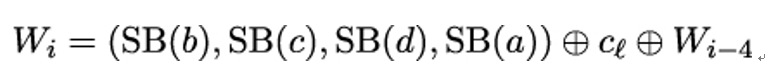
Each round key consists of four consecutive words Wi:
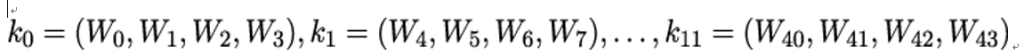
For the other key lengths, the expansion algorithm has to be slightly adjusted: a 192-bit key consists of six 32-bit words, and a 256-bit key consists of eight 32-bit words; therefore, for a 192-bit key, the expanding algorithm changes if i is a multiple of six, and for a 256-bit key, it changes if i is a multiple of eight.
Finally, if the key length is 256, there is one more modification of the preceding algorithm: if i = 4 mod 8, then
We can now formulate the key expansion algorithm in full generality: Suppose k has n bits, where n ∈{128,192,256}. Depending on n, we are going to do r rounds, where r ∈{10,12,14}, and we are going to expand k into r + 1 round keys of 128 bits each.
For this, we first separate k into N 32-bit words W0,…,WN−1, where N = n∕32. Now we generate more 32-bit words Wi for N ≤ i ≤ 4r + 3 using the following algorithm:
- If i ≥ N is a multiple of N, let Wi−1 = (a,b,c,d), where a,b,c,d are bytes. Then
where ℓ = i∕N − 1 and cℓ as in Table 14.1.
- If N = 8 and i = 4 mod 8,
- In all other cases,
Because our space is limited, this concludes our tour of the AES block cipher. There is much more that could be said about AES, especially how some parts of it are motivated by the need to be resistant against certain generic attacks (linear cryptanalysis and differential cryptanalysis) against block ciphers. If you are interested in these topics, please refer to the book [46] written by the two designers of AES.
We now leave the nuts and bolts of constructing a secure block cipher and turn to the following question: given a secure block cipher, how we should deal with a large number of (possibly identical) plaintext blocks?
