Overall structure – Block Ciphers and Their Modes of Operation
14.3.1 Overall structure
AES has a fixed block length of 128 bits and, as required by the initial call for algorithms, a flexible key length of 128, 192, or 256 bits. AES is a substitution-permutation network consisting of 10, 12, or 14 rounds, depending on the key length.
The 128 plaintext bits are arranged in a (4,4) state matrix A, where each entry aij holds a byte of data. These bytes are treated as elements of the finite field 𝔽2[X]∕P with 28 elements, where P is the irreducible polynomial
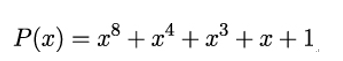
(see Section 7.6, Finite fields in Chapter 7, Public-Key Cryptography). Other than in the DES algorithm, the bytes always retain their structure and are never broken up into smaller parts. This has proven to be advantageous on eight-bit platforms (see [46]).
14.3.2 Round function
The round function f of the AES algorithm has four components (see also Figure 14.5):
- SubBytes: This is the only non-linear component of the round function. It implements the substitution part in the substitution-permutation network. In software, SubBytes is implemented via a lookup table, but the table entries can be explained mathematically:
First, each byte b in the state matrix is replaced by its multiplicative inverse in 𝔽2[X]∕P. The zero byte 00 is mapped onto itself:
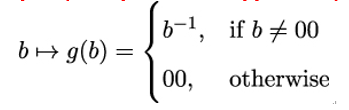
This map has been shown in [133] to have good resistance against differential and linear cryptanalysis.
However, this simple algebraic expression in itself would lead to a very simple algebraic expression for the complete round function, which could be used to mount other attacks. Therefore the non-linear component g is followed by an affine transformation f. In this transformation, the input byte b is multiplied bitwise by a fixed (8,8) matrix M, and a constant byte v is added afterward:
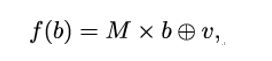
where

Summing up, the SubBytes part of the round function is given by
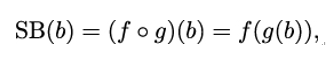
with f and g as defined above.
- ShiftRows: The ShiftRows transformation is a simple operation that cyclically shifts the bytes of row i in the state matrix by i places to the left; that is, row 0 is not shifted, row 1 by one place, and so on (see also Figure 14.5). As is pointed out in [46], the shifts for the different rows are different in order to achieve optimal diffusion.
- MixColumns: Like ShiftRows, this step is part of the permutation component of the round function. MixColumns mixes the entries of each column vector →vj of the state matrix by treating the bytes bij within →vj as coefficients of a polynomial pj of degree ≤ 3:
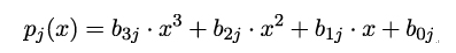
The mixing is achieved by multiplying each pj by a fixed polynomial
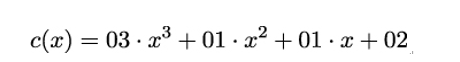
Like the coefficients of pj, the coefficients of c(x) are bytes; therefore, they are written as hexadecimal numbers. The multiplication of pj and c is done modulo x4 + 1, so that the resulting polynomial is of degree ≤ 3 again and its coefficients can be used to populate an output column vector consisting of four bytes again. The coefficients of the polynomial c were carefully chosen to allow for efficient multiplication.
As is shown in [46], p.39, the multiplication by c(x) modulo x4 + 1 can be represented in matrix form by the formula

- AddRoundKey: As the last step in each round, a round key ki, where 1 ≤ i ≤ r is added to the current block. In addition, before the first round, a round key k0 is added to the plaintext via bitwise XOR.
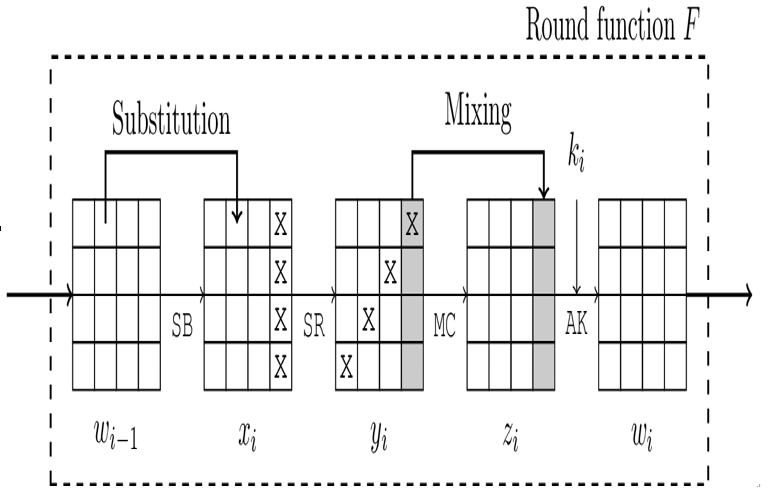
Figure 14.5: Structure of the AES round function. wi−1 is the word described by the state before round i. In the last round, the MixColumns step is omitted
