Pseudorandom permutations – Block Ciphers and Their Modes of Operation
14.2.4 Pseudorandom permutations
Simply put, a permutation is a function that rearranges the order of elements in a set. A random permutation is a permutation that is randomly chosen from all possible permutations for a given set. A pseudorandom permutation looks like a random permutation to any polynomial-time observer, but is actually a deterministic algorithm.
Let f : {0,1}n ×{0,1}b →{0,1}b again be a length-preserving keyed function that can be efficiently computed; that is, Alice and Bob can compute it in polynomial time. f is a keyed permutation if, for every key k, the function fk is a bijection. That is, each element in fk’s domain is mapped to exactly one element in fk’s range, and each element in fk’s range has exactly one preimage in fk’s domain (see Figure 14.2 and also Figure 4.3).
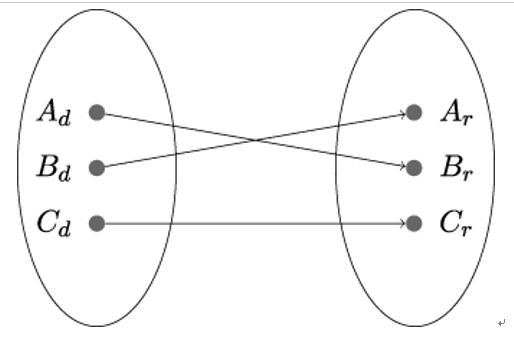
Figure 14.2: Example of a bijective function
Formally, a keyed permutation fk(x) is considered efficient if it can be computed in polynomial time and there is a polynomial-time algorithm for computing the inverse fk−1(x). The length of fk(x)’s input and output – also referred to as block size – is typically identical, but the length of key k can be different from the block size.
The keyed permutation fk(x) is pseudorandom if an efficient adversary, that is, an algorithm running in polynomial time, cannot distinguish fk from a randomly chosen permutation f. When fk is used in cryptographic algorithms such as symmetric-key encryption, Alice and Bob need to compute the inverse fk−1 in addition to fk itself. This could, however, negatively affect security despite fk being pseudorandom. Consequently, if fk is used in a cryptographic algorithm, it must be a strong pseudorandom permutation. fk is called a strong pseudorandom permutation if no efficient adversary can distinguish fk from a permutation chosen at random even if the adversary has oracle access to fk−1.
Basically, pseudorandom permutations are also pseudorandom functions. On the other hand, a pseudorandom function is a pseudorandom permutation if it is a bijection.
Block ciphers, because they must be invertible, are typically modeled as strong pseudorandom permutations. That is, standardized block ciphers are generally assumed to behave like strong pseudorandom permutations. Cryptographers make this assumption so they can formally analyze cryptographic mechanisms that are based on block ciphers.
